알고리즘
BOJ) 동전 1. Python
1일1공부실천하자
2024. 6. 24. 21:53
https://www.acmicpc.net/problem/2293
입력 예제로 들어온 값으로 예를 들어보자
3 10
1
2
5
1,2,5의 동전으로 10을 만들 수 있는 경우의 수는 몇 개인가?
우리가 생각해보아야할 것은
- 1의 동전으로 몇 개를 만들 수 있는가.
- 1과 2의 동전으로 몇 개를 만들 수 있는가
- 1과 2와 5의 동전으로 몇 개를 만들 수 있는가
여느 dp문제와 헷갈린 점이
2원짜리 동전은 1원짜리 동전으로 나눌 수 있으니 이를 이용해 dp를 작성하면 된다 생각했다.
하지만 이는 문제를 잘못 쪼갠 것이다.
1원으로 k원을 만들 수 있는 경우의 수,
1과 2원으로 k원을 만들 수 있는 경우의 수,
1과 2와 5원으로 k원을 만들 수 있는 경우의 수
이런 작은 문제들로 쪼개야한다.
우선 1원으로 0원부터 k원(10원)을 만들 수 있는 경우의 수는 다음과 같다.
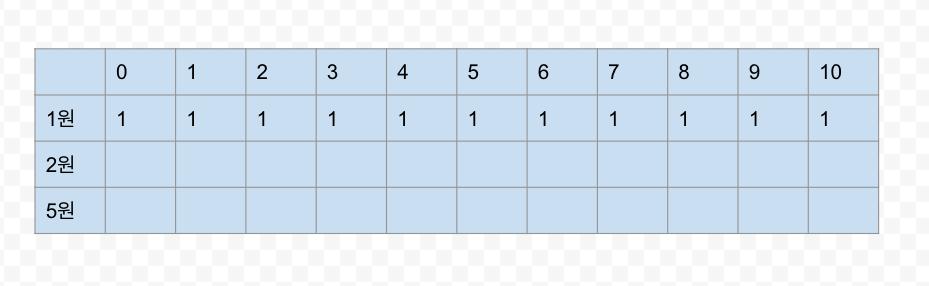
0원은 동전을 아예 제출하지 않으면 0원을 만들 수 있으니 1가지의 경우의 수가 존재한다.
1원과 2원은 다음과 같다.
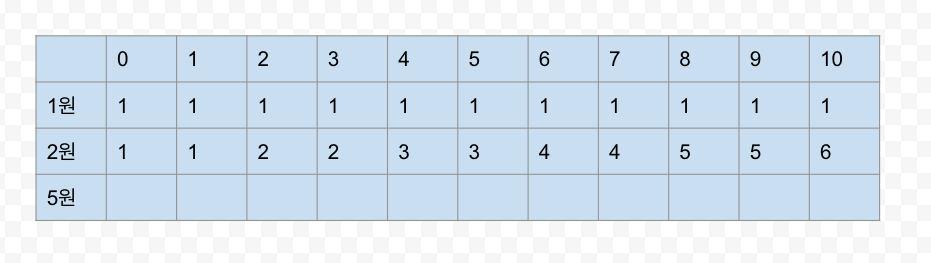
2원의 경우 현재 x원을 만들 수 있는 경우의 수는 다음과 같다.
- 2원으로 x원을 만들 수 있는가?
- 맞다면 경우의 수 + 1
- 1원으로 x원을 만들 경우의 수 ( +1)
- 2원과 1원으로 x원을 만들 경우의 수
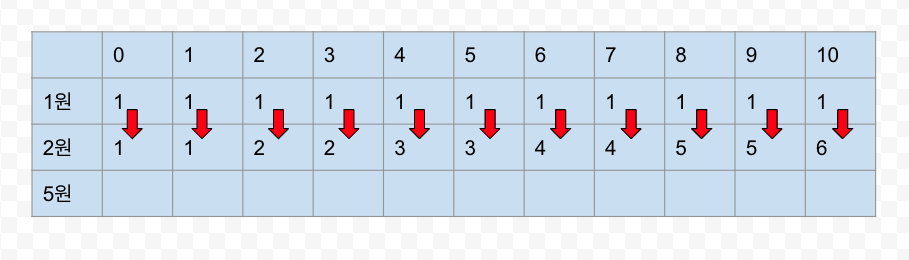
즉, 위 사진 같이 위 1원으로 만든 경우의 수를 상속받는다.
여기서 2원과 1원으로 x원을 만들 수 있는 경우의 수를 구하는 과정은 문제를 더 쪼개보면 가능하다.
x를 4라고 가정한다면,
- 1원으로 4원을 만드는 경우의 수를 상속받으며
- 1원과 2원으로 2를 만드는 경우의 수를 더한다.
이를 5원까지 적용해보면 다음과 같다.
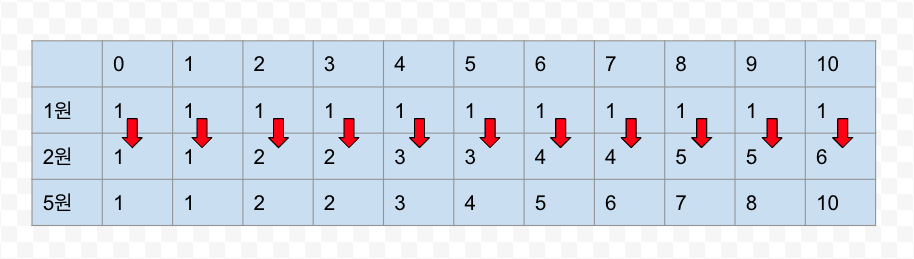
위에는 어떤 공식이 있는데,
x원이라 가정했을 때, dp의 x - coin 인덱스 번째를 더한다.
이를 점화식으로 표현하면 다음과 같다.
for num in arr:
for idx in range(num, k + 1):
dp[idx] = dp[idx] + dp[idx - num]
n, k = map(int, input().split())
arr = []
dp = [0] * (k+1)
dp[0] = 1
for _ in range(n):
arr.append(int(input()))
for num in arr:
for idx in range(num, k + 1):
dp[idx] = dp[idx] + dp[idx - num]
print(dp[k])