파이썬)구간 합 구하기 - BOJ(세그먼트 트리)

https://www.acmicpc.net/problem/2042

2042번: 구간 합 구하기

 

우선 세그먼트 트리의 경우 힙 정렬 알고리즘과 상당히 비슷하다.

대신 단순히 트리를 만들어 정렬하는 힙정렬 알고리즘과 달리 세그먼트 트리는 구간 합, 최소, 최대를 구하는데 최적화가 되어있다.

이번 백준 2042번 구간 합 구하기는 도저히 스스로 풀 수가 없어서 다른 이의 코드를 참조했다.

우선 코드를 보자. 

import sys
input = sys.stdin.readline

# 수의 개수, 수 변경 횟수, 구간의 합 횟수
n,m,k = map(int,input().split())
num = [int(input()) for _ in range(n)]

# 세그먼트 트리
# seg_tree[1] : 모든 노드의 합
# seg_tree[2] : 0~n//2번 노드의 합
# seg_tree[3] : n//2+1~n번 노드의 합
seg_tree = [0 for _ in range(4*n)]

# 1. 세그먼트 트리 만들기
# seg_tree[x] 값 구하기
def build_tree(x,left,right):
    if left == right:
        seg_tree[x] = num[left]
        return seg_tree[x]
    mid = (left + right)//2
    left_value = build_tree(2*x,left,mid)
    right_value = build_tree(2*x+1,mid+1,right)
    seg_tree[x] = left_value + right_value
    return seg_tree[x]

build_tree(1,0,n-1)

# 2. 세그먼트 트리로 구간 합 구하기
# b~c구간합 구하기
# 트리의 구간 left~right
# 현재 노드 x
def find_tree(b,c,x,left,right):
    # 구하고 싶은 구간(b~c)가 현재 트리 구간에 포함 X
    if c < left or right < b:
        return 0
    # 구하고 싶은 구간(b~c) 안에 현재 트리 포함
    if b <= left and right <=c:
        return seg_tree[x]
    # 구간이 겹치는 경우
    mid = (left + right)//2
    left_value = find_tree(b,c,x*2,left,mid)
    right_value = find_tree(b,c,x*2+1,mid+1,right)
    return left_value + right_value

# 3. 세그먼트 트리 값 업데이트
# 인덱스 idx의 값을 val로 바꾸기
def update_tree(x,left,right,idx,val):
    # 길이 1인 구간
    if left == right == idx:
        seg_tree[x] = val
        return
    # 현재 구간에 idx가 포함 X
    if idx < left or right < idx:
        return
    
    mid = (left + right)//2
    # 왼쪽 자식 업데이트
    update_tree(x*2,left,mid,idx,val)
    # 오른쪽 자식 업데이트
    update_tree(x*2+1,mid+1,right,idx,val)
    
    # 업데이트 된 자식 노드를 통해 현재 노드 업데이트
    seg_tree[x] = seg_tree[x*2] + seg_tree[x*2+1]
    
for _ in range(m+k):
    a,b,c = map(int,input().split())
    # b번째 수를 c로 바꾸기
    if a == 1:
        update_tree(1,0,n-1,b-1,c)
    # b번째 수부터 c번째 수까지 합 구하기
    else:
        s = find_tree(b-1,c-1,1,0,n-1)
        print(s)

우선 힙 정렬과 마찬가지로 트리구조를 만들어 각 노드에 숫자를 저장한다.

노드의 숫자는 자신의 자식 노드들(왼쪽 자신노드와 오른쪽 자식노드)의 합이다.

build_tree의 초기 인자인 1,0,n-1을 기준으로 트리 생성함수를 살펴보자.

우선 build_tree의 초기값은 세그먼트 트리 배열인 seg_tree의 첫번째(인덱스 0이 아닌 인덱스 1)을 구하는 인자다.

아까 말했듯이 각각의 노드는 자신의 왼쪽 자식노드 + 오른쪽 자식노드의 값이다.

build_tree의 인자값인(최상위 노드) 노드또한 마찬가지이다.

그럼 이 노드의 왼쪽 자식노드를 구하는 코드를 보자.

최상위 노드의 왼쪽 노드가 생성되었다.

하지만 이 노드(최상위 노드의 왼쪽 노드) 또한 자식의 왼쪽 노드 + 오른쪽 노드이다.

편의상 최상위 노드부터 1번 ~4번으로 설정했다.

4번 노드까지 내려온 상태를 살펴보자.

def build_tree(x,left,right):
    if left == right:
        seg_tree[x] = num[left]
        return seg_tree[x]
    mid = (left + right)//2
    left_value = build_tree(2*x,left,mid)
    right_value = build_tree(2*x+1,mid+1,right)
    seg_tree[x] = left_value + right_value
    return seg_tree[x]

build_tree(1,0,n-1)

이때 인자 값은 build_tree(8,0,0)이 된다.

따라서 left == right 조건문에 따라 seg_tree[8] = num[0]가 된다.

4번 노드를 num[0]인 1로 업데이트 한다.

다시 right를 구해야한다.

right는 left와 마찬가지로 재귀함수를 오른쪽 자식노드의 값을 구하며 그 자식 노드 또한 왼쪽 자식 + 오른쪽 자식노드의 값을 통해 업데이트되는 것이다.

정리를 하자면 최상단을 구하기 위해선 왼쪽 자식 노드(2번 )와 오른쪽 자식노드를 구하고 2번 노드는 왼쪽 자식노드는 오른쪽 자식노드와 왼쪽 자식노드를 구한다.

seg_tree가 완성된 시점의 트리를 살펴보자.

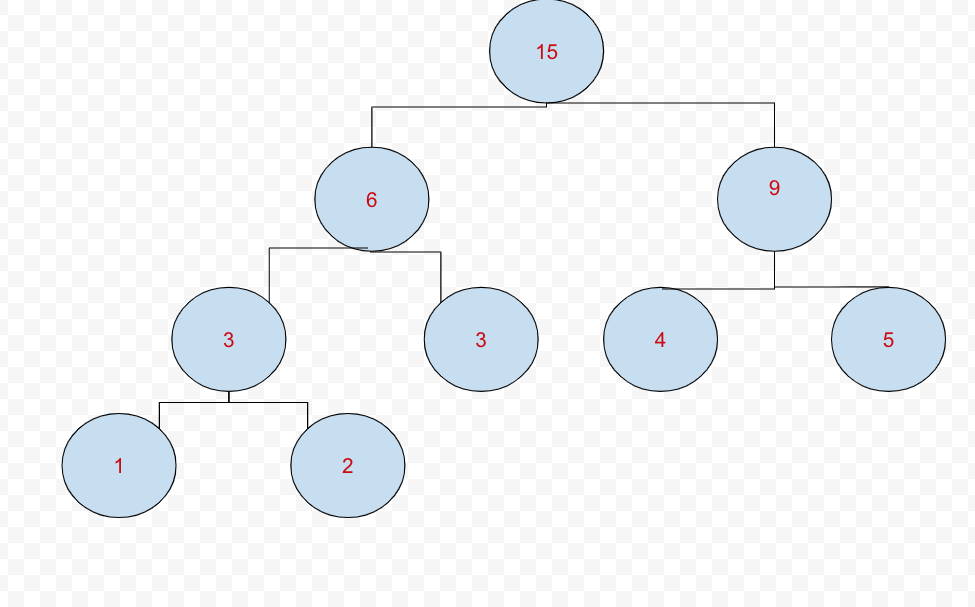
이를 배열로 나타낸다면 최상단 노드가 1번 인덱스(0번 인덱스가 아님)이고, 다음 줄 맨 왼쪽부터 +1씩 인덱스가 늘어난다.그럼 어떻게 이를 배열로 만들까.

 

그럼 어떻게 이를 배열로 나타낼까

우선 각각의 노드 값과 그 인덱스를 살펴보자.

15 == 1인덱스

6 == 2번 인덱스

9 == 3번 인덱스

3 == 4번 인덱스

3 == 5번 인덱스

4 == 6번 인덱스

5 == 7번 인덱스

1 == 8번 인덱스

2 == 9번 인덱스

무언가 규칙이 보이지 않는가?

자, 다시 위에 언급했던 말을 살펴보자.

아까 말했듯이 각각의 노드는 자신의 왼쪽 자식노드 + 오른쪽 자식노드의 값이다.

그럼 1번 인덱스는 2번 인덱스.+ 3번 인덱스이다.

2번 인덱스는 4번 인덱스 + 5번인덱스이다.

4번 인덱스는 8번 인덱스 + 9번 인덱스이다.

즉, seg_tree[idx]는 seg_tree[idx *2] + seg_tree[idx* 2 + 1]이다.

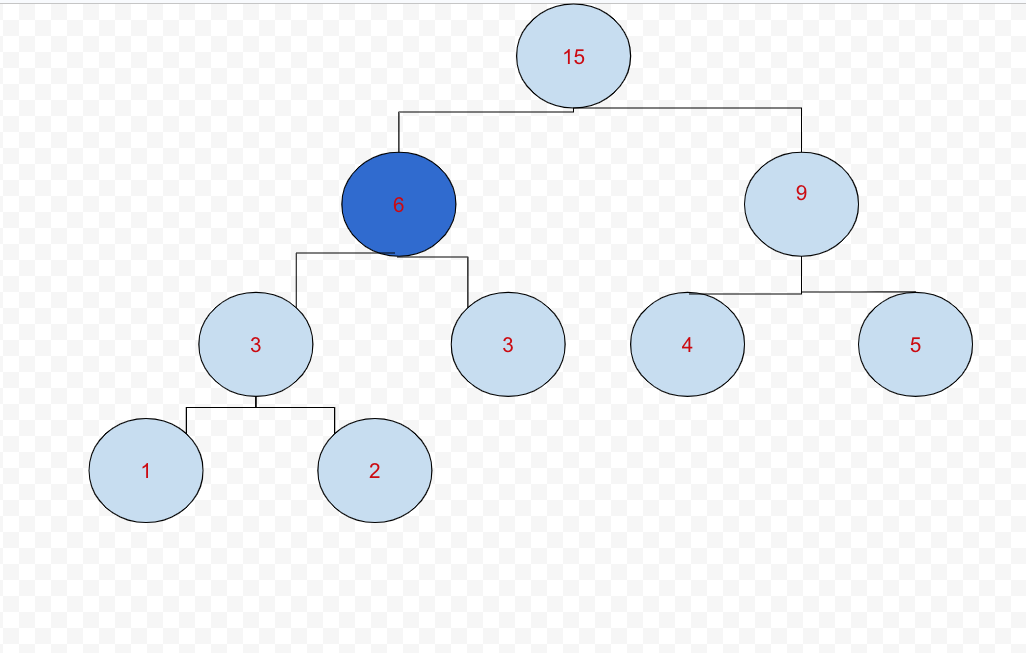
구간합 구하기는 b인덱스를 c값으로 바꾸는 숫자의 업데이트가 일어난다.

만약 seg_tree의 2번 인덱스가 바뀐다고 생각해보자.

2번 인덱스의 값이 바뀐다면 2번 인덱스를 포함하는 모든 구간의 합 노드들을 갱신해야한다.

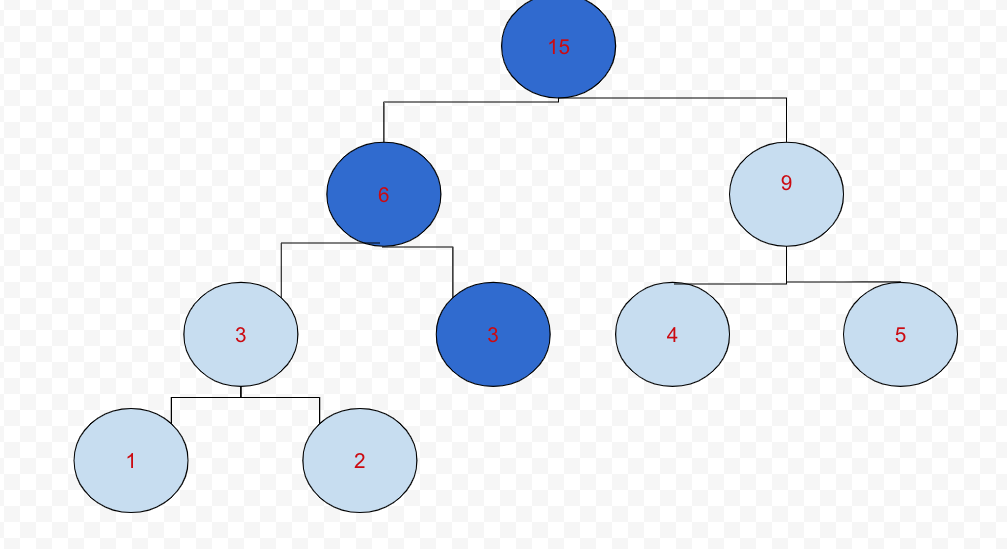
마찬가지로 left right값을 구해 인덱스를 갱신해야 한다.

def update_tree(x,left,right,idx,val):
    # 구간에 데이터 1개, 그 데이터가 idx에 해당
    if left == right == idx:
        seg_tree[x] = val
        return
        
    # 현재 구간에 idx가 포함 X
    if idx < left or right < idx:
        return
    
    # 자식 노드에 idx가 포함된다면 부모 노드도 변한다
    mid = (left + right)//2
    # 왼쪽 자식 업데이트
    update_tree(x*2,left,mid,idx,val)
    # 오른쪽 자식 업데이트
    update_tree(x*2+1,mid+1,right,idx,val)
    
    # 업데이트 된 자식 노드를 통해 현재 노드 업데이트
    seg_tree[x] = seg_tree[x*2] + seg_tree[x*2+1]

 

 

구간 합을 구하는 과정은 매우 간단하다.

def find_tree(b,c,x,left,right):
    # 구하고 싶은 구간(b~c)가 현재 트리 구간에 포함 X
    if c < left or right < b:
        return 0
    # 구하고 싶은 구간(b~c) 안에 현재 트리 포함
    if b <= left and right <=c:
        return seg_tree[x]
    # 구간이 겹치는 경우
    mid = (left + right)//2
    left_value = find_tree(b,c,x*2,left,mid)
    right_value = find_tree(b,c,x*2+1,mid+1,right)
    return left_value + right_value

 

bfs,dfs, 이분탐색, 투포인터 등의 알고리즘을 보다 세그먼트 트리로 넘어오니 난이도가 확 달라진 것이 느껴진다..

너무 어렵다..