THREEJS로 인테리어 기능

안녕하세요.

이번 팀 프로젝트로 진행한 "IDesign"에서 저는 THREEJS를 활용한 인테리어 기능과 대시보드 페이지를 맡았습니다.

제가 설명/소개해드릴 부분은 THREEJS에 대한 내용이 아닌, "Three.js를 이용해 어떤 기능을 어떻게 구현했나"입니다.

Three.js에 대해 다들 한 번쯤 들어보셨을텐데요, 블로그의 글이 구현 방법에 초점이 맞춰진 만큼 Three.js에 대한 것은 간단하게 소개하고 넘어가겠습니다. Three.js에 대해 자세히 알고 싶다면 공식문서를 읽어보길 추천합니다.

1. THREE.JS 소개

웹에서의 3D 그래픽은 매우 까다로운 영역이었습니다. 그러나 Three.js는 이 복잡한 작업을 쉽게 만들면서도 강력한 성능을 제공합니다.

제가 Three.js에 관심을 갖게 된 것은 이 프로젝트를 진행하면서는 아닙니다.

이 프로젝트를 진행하기 전, "HandGestureNodeMover"라는 개인 프로젝트를 진행했었습니다. 이 프로젝트는 Figma API를 이용해 디자인을 Web Canvas에 그린 후, 이를 손동작으로 움직일 수 있게하는 프로젝트입니다. 하지만 CPU만으로 매 프레임마다 수많은 작업을 진행하기에는 한계가 있었고 WebGL을 사용하는 Three.js에 관심을 갖게 되었습니다.

WebGL은 웹 브라우저에서 GPU를 활용하여 복잡한 3D 그래픽을 그릴 수 있도록 도와주는 API입니다. 하지만 웹에서 GPU를 사용하기 위해서는 C++같은 타 언어를 사용해야하는 어려움이 있습니다. 하지만 Three.js는 복잡한 WebGL API를 매우 간단하게 사용할 수 있게 해주며 활발한 커뮤니티로 방대한 자료가 뿌려져있습니다.

Three.js는 네가지 기본 구성 요소를 갖습니다

Scene은 3D노드들이 위치한 공간입니다. 모든 3D 노드(물체)들은 이 Scene위에 생성됩니다. 즉, "화면"이라 생각하시면 됩니다.

Camera는 Scene을 바라보는 시점입니다. threejs는 기본적으로 화면에 보여지지 않는 부분은 렌더링하지 않는"frustum culled"를

사용하고 있기에 카메라로 씬의 일부분을 비추어야 해당 씬을 렌더링하여 사용자에게 보여줍니다.

renderer는 Scene, Camera, Light 등의 3D 노드들을 실제 화면에 그려주는 역할을 합니다. 렌더러는 장면을 카메라의 시점에서 그려 최종적으로 사용자에게 보이는 화면을 생성합니다.

Light는 씬에서 빛을 조절하는 역할입니다. 다양한 빛을 생성하여 노드에 비추어 해당 노드가 어떻게 보일지를 결정합니다. threejs에서 Scene과 Camera를 만들면 기본적으로 검은 화면이 나옵니다. 이는 빛이 없기 때문에 불이 꺼진 방에 있는 것과 같습니다.

이들은 모두 Three.js의 기본요소이며 Light를 제외하고는 반드시 하나씩은 존재해야 합니다.

또한 물체에 대한 구성요소가 있습니다.

Geometry는 노드의 모양과 구조를 정의합니다. 즉, 지오메트리는 물체의 "뼈대"와 같습니다. 위 코드에서 사용한 육면체를 생성하는 BoxGeometry와 평면을 생성하는 PlaneGeometry등이 있습니다.

Material은 재질을 결정합니다. 즉 어떤 물체가 어떻게 보일지, 표면이 빛을 어떻게 반사하는지 등에 대한 설정입니다. 이는 Light와 밀접한 관계가 있습니다. 어떤 Light를 사용하느냐에 따라 개발자가 정의한 재질을 그대로 보여줄 수도 있고, 달리 보이게 만들수도 있습니다.

Mesh는 Geometry와 Material을 결합한 객체로 Scene에 배치할 수 있는 3D 노드입니다.

즉 어떤 물체를 화면에 나타내고 싶다면 다음과 같이 코드를 작성할 수 있습니다.

import * as THREE from 'three';

const scene = new THREE.Scene();
const camera = new THREE.PerspectiveCamera( 75, window.innerWidth / window.innerHeight, 0.1, 1000 );

const renderer = new THREE.WebGLRenderer();
renderer.setSize( window.innerWidth, window.innerHeight );
renderer.setAnimationLoop( animate );
document.body.appendChild( renderer.domElement );

const geometry = new THREE.BoxGeometry( 1, 1, 1 );
const material = new THREE.MeshBasicMaterial( { color: 0x00ff00 } );
const cube = new THREE.Mesh( geometry, material );
scene.add( cube );

camera.position.z = 5;

function animate() {

	cube.rotation.x += 0.01;
	cube.rotation.y += 0.01;

	renderer.render( scene, camera );

}

2. 프로젝트에 녹여낸 기능과 구현 방식

Three.js에 대해 간단하게 소개한 대신 "어떻게 구현했는지"에 대해 자세히 설명하겠습니다.

우선 모든 기능은 "방"에서 시작됩니다.

위 이미지는 2D 시점이며 2D 시점에서의 방은 벽과 바닥으로 구성됩니다.

더 자세히는 방의 모양을 변경할 수 있는 CircleGeometry와 면적,길이 등의 정보를 나타내는 TextGeometry도 있습니다.

즉, 단순한 하나의 방에 여러개의 객체(물체)가 존재합니다.

글을 읽기 전 헷갈리실 만한 부분에 대해 설명드리겠습니다. 아래 사진상의 빨간색 축이 x축, 파란색 축이 z축이며 녹색 축이 y축입니다.

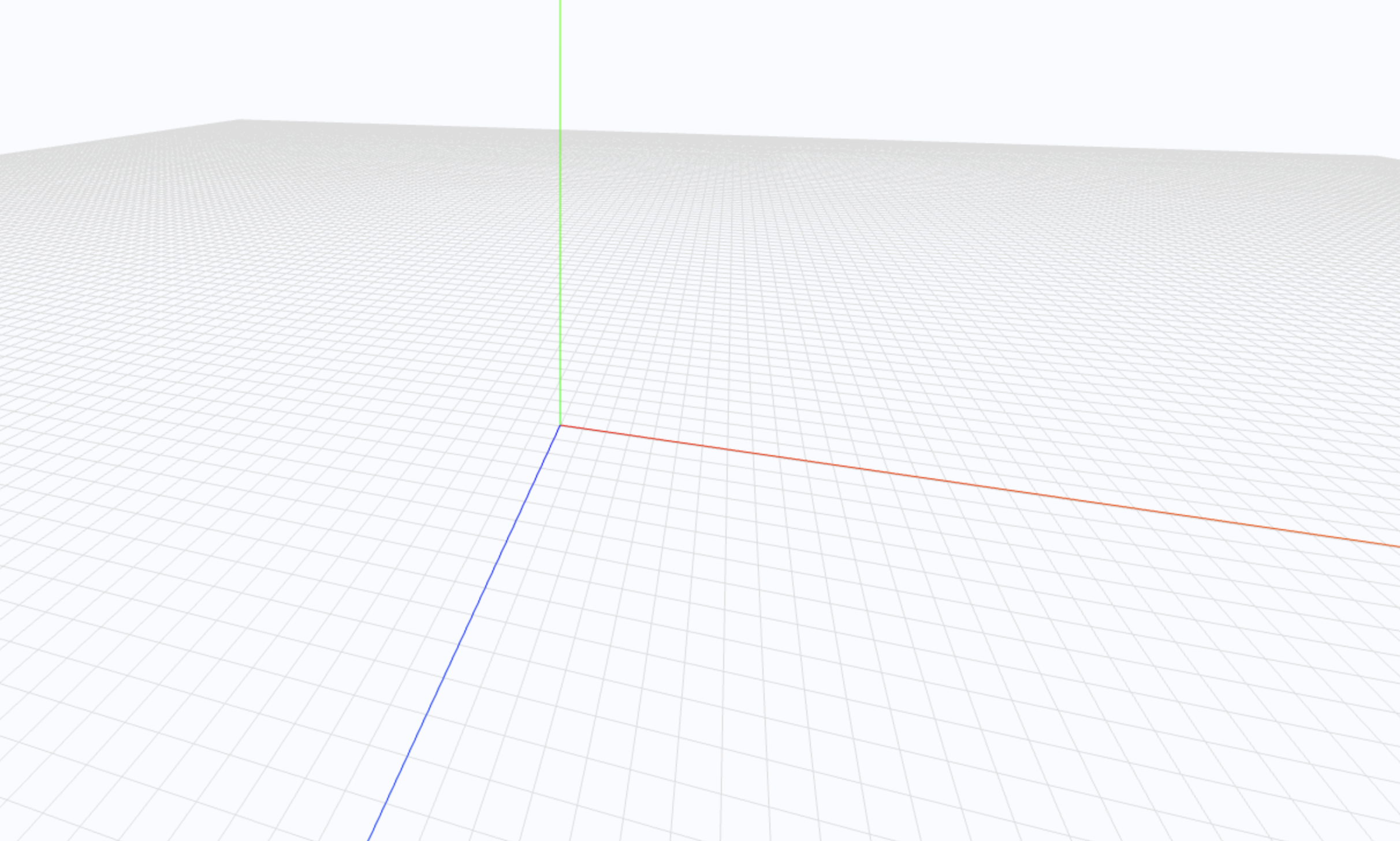
2-1. 바닥

바닥은 방의 가장 핵심이 되는 영역입니다. 복잡한 계산은 없지만 해당 영역이 방을 이루는 가장 근본적인 물질이 되는거죠.

방의 생성은 사용자가 누른 지점부터 다시 한번 더 사용자가 누른 지점까지의 영역입니다. 그 영역을 바닥으로 채워 사용자가 한 눈에 알아보기 쉽도록 합니다. 사진상의 우드(wood)스타일의 영역이 바로 바닥입니다.

단순히 평면 사격형의 바닥은 PlaneGeometry로 쉽게 생성할 수 있습니다. 하지만 저희의 목적은 사각형이 아닌 다각형에 있었고 그 형태또한 사용자가 정의할 수 있도록하는 것에 있었습니다.

때문에 points라는 좌표를 가진 좌표들로 Geometry를 만들 수 있는 ShapeGeometry를 선택했습니다.

const floorTexture = new THREE.TextureLoader().load(floorPaper);

export const floorMaterial = new THREE.MeshBasicMaterial({
  map: floorTexture,
  side: THREE.FrontSide,
});


export class D2Floor {
  constructor({ points, height, center, name }) {
    //바닥
    const shape = new Shape({ points });
    const geometry = new THREE.ShapeGeometry(shape);

    //바닥 material
    geometry.computeBoundingBox();
    const boundingBox = geometry.boundingBox;
    const offset = boundingBox.min;
    const range = boundingBox.max.clone().sub(offset);
    const uvAttribute = geometry.attributes.uv;
    for (let i = 0; i < uvAttribute.count; i++) {
      const x = (uvAttribute.getX(i) - offset.x) / range.x;
      const y = (uvAttribute.getY(i) - offset.y) / range.y;
      uvAttribute.setXY(i, x, y);
    }
    uvAttribute.needsUpdate = true;

    // Mesh 생성
    const material = height ? ceilingMaterial : floorMaterial;
    const mesh = new THREE.Mesh(geometry, material);
    mesh.name = floorName;
    mesh.renderOrder = 1;
    mesh.rotation.x = -Math.PI / 2;
    const y = height ? height : floorY;
    mesh.position.set(-center.x, y, -center.z);
    mesh.userData = {
      ...mesh.userData,
    };
    return mesh;
  }
}

export class Shape extends THREE.Shape {
  constructor({ points }) {
    const shape = super();
    shape.moveTo(points[0].x, -points[0].z); // z축을 y축으로 사용하여 평면 도형 정의
    for (let i = 1; i < points.length; i++) {
      shape.lineTo(points[i].x, -points[i].z);
    }
    shape.lineTo(points[0].x, -points[0].z); // 마지막 점을 처음 점에 연결

    return shape;
  }
}

평범한 바닥을 원하면 단순한 material을 사용하면 되지만 저희는 wood스타일의 바닥을 원했습니다. 때문에 이미지를 가져와 텍스쳐로 로딩하는 과정을 거쳐야했죠. 하지만 어떤 형태가 정해지지 않았기 때문에 텍스쳐가 바로 적용되지 않습니다.

해당 코드처럼 UV좌표를 계산하여 설정을 해야 합니다.

2-2. 외벽

사진 상의 회색의 공간이 외벽입니다. 나무 모양의 바닥의 각 변에는 외벽이 존재합니다. 이 벽의 두께를 offset라 하겠습니다.

점 x1,z1에서 x2,z2로 이어진 선에서 offset만큼 떨어진 위치는 어떻게 될까요?

문제 1

단순하게 생각하면 방의 각 꼭지점 중 하나인 x1,z1 좌표에서 각각 offset만큼을 더한 값이 되는데, 이 방법을 네 변 전체에 적용하려면, 또한 변의 각도에 따라 좀 더 계산이 필요합니다. 우리는 이를 해결하기 위해 두 점 사이의 벡터에 수직인 벡터를 활용할 수 있습니다

const getPerpendicularVector = (dx, dz) => {
  const distance = 25;
  // 변의 방향 벡터 (dx, dz)에 수직인 벡터
  // x축 우세 시, z축 방향으로 이동
  // z축 우세 시, x축 방향으로 이동
  return Math.abs(dx) > Math.abs(dz)
    ? { x: 0, z: -Math.sign(dx) * distance }
    : { x: Math.sign(dz) * distance, z: 0 };
};

// 각 변에서 ±25만큼 떨어진 점 계산 함수
export const calculateOffsetPoints = (p1, p2) => {
  const dx = p2.x - p1.x;
  const dz = p2.z - p1.z;

  // 방향 벡터에 수직인 벡터 계산
  const perpendicular = getPerpendicularVector(dx, dz);

  // 새로운 점 계산
  const offsetPoint1 = {
    x: p1.x + perpendicular.x,
    y: p1.y,
    z: p1.z + perpendicular.z,
  };

  const offsetPoint2 = {
    x: p2.x + perpendicular.x,
    y: p2.y,
    z: p2.z + perpendicular.z,
  };

  return [offsetPoint1, offsetPoint2];
};

getPerpendicularVector 함수는 수직 벡터 계산 함수입니다.

먼저, 두 점 x1,z1과 x2,z2 사이의 선분에 대해 수직인 벡터를 계산하는 함수를 작성했습니다. 여기서 중요한 것은 x축과 z축 방향을 고려해, 각각의 우세한 축에 따라 적절히 수직 벡터를 구하는 방식입니다. 이 함수에서는 두 점 p1, p2의 차이인 dx와 dz를 통해 변의 방향을 알 수 있습니다. 이에대해 잘 이해가 안되실텐데요, 두 점 p1,p2를 연결한 선이 있습니다. 이 선의 방향은 두 점의 x축 좌표와 z축 좌표의 차이로 결정됩니다. 이는 벡터의 정의에 있습니다. 벡터는 두 점 사이의 상대적인 위치 변화를 나타내기 때문에, 좌표 차이를 통해 그 방향과 크기를 계산할 수 있습니다.

만약 x축 쪽 차이(dx)가 크다면, z방향으로 수직 벡터를 구하고, 반대로 z축 쪽 차이(dz)가 크다면 x축 방향으로 수직 벡터를 구하게 됩니다.

calculateOffsetPoints 함수는 벽의 두께만큼 떨어진 새로운 점들을 계산하는 함수입니다. 두 점 사이에 수직 벡터를 계산한 후, 그 수직 벡터를 각 점에 더해 새로운 점들의 좌표를 구할 수 있습니다.

문제 2

하지만 단순히 벽의 두께만큼의 벽을 세우는 것은 문제가 있었습니다.

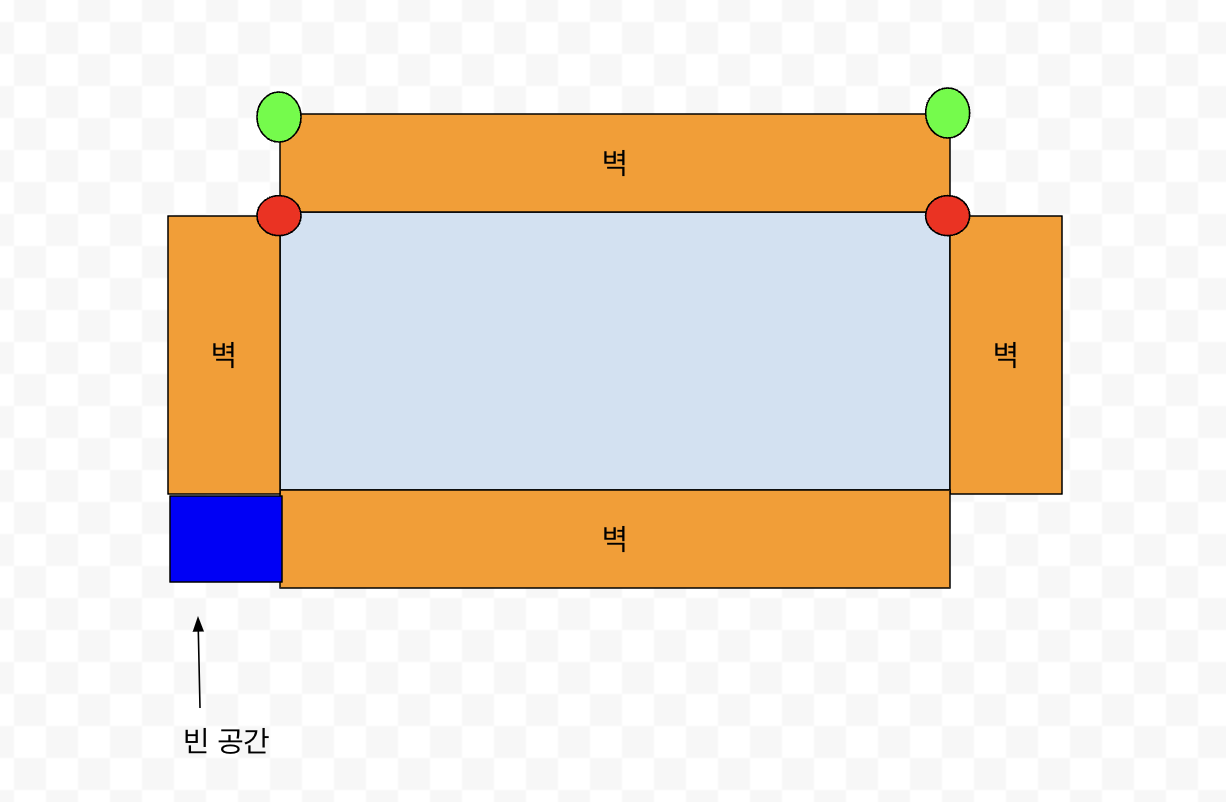
위 계산대로라면 각각의 빨간색 지점의에서 offset만큼 떨어진 곳이 형광색 지점입니다. 하지만 이런 방식은 문제가 있습니다. 위 사진의 파란색 영역처럼 애매하게 빈 공간이 생기게 됩니다.

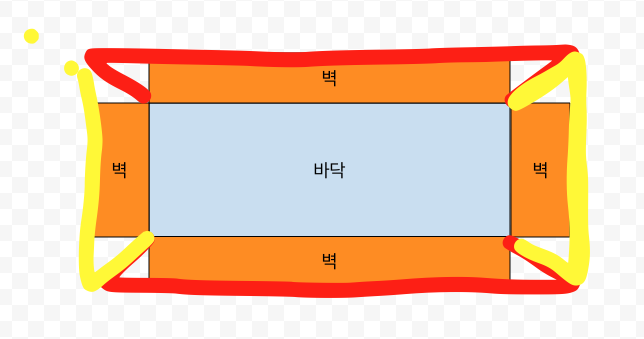
때문에 모서리 부분 또한 채울 수 있도록 다음과 같이 외벽을 마름모 모양으로 잡아주면 해결됩니다.

그러나 문제는 또 한가지 남아 있었습니다.

문제 3

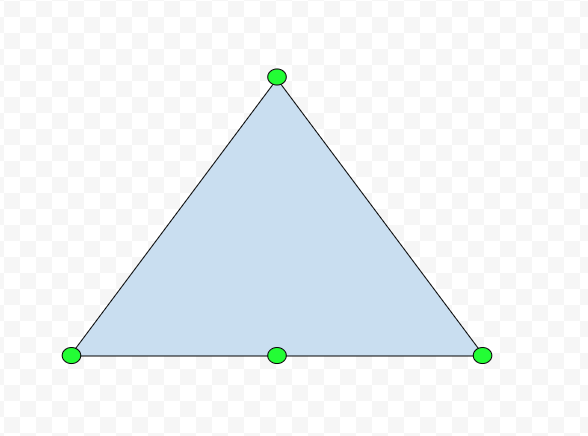
만약 사용자가 정의한 도형이 삼각형이고 각 꼭지점 사진과 같습니다. 이때 마름모 꼴의 외벽을 적용한다면

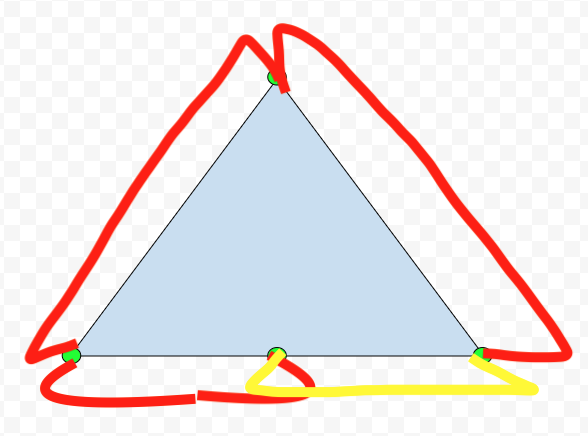
위 사진과 같이 겹치는 부분이 생기게 되거나 혹은 빈 공간이 생기게 됩니다.

해결 방법

이러한 문제점에 저희는 골머리를 앓아야했습니다. 그리고 해답을 찾아냈습니다.

저희는 두 점 x1,z1과 x2,z2로 offset만큼 이동한 좌표 dx2,dz2를 구할 수 있습니다. 또한 x2,z2와 x3,z3로 dx2,dz2를 구할 수 있습니다.

그렇다면 방이 어떤 모양이든 외벽이 겹치지 않으면서 빈 공간이 없다면 어떻게 해야할까요?

방의 변에서 offset만큼 떨어진 dx1,dz1와 dx2,dz2의 만나는 지점을 기준으로 외벽을 생성하면 됩니다.

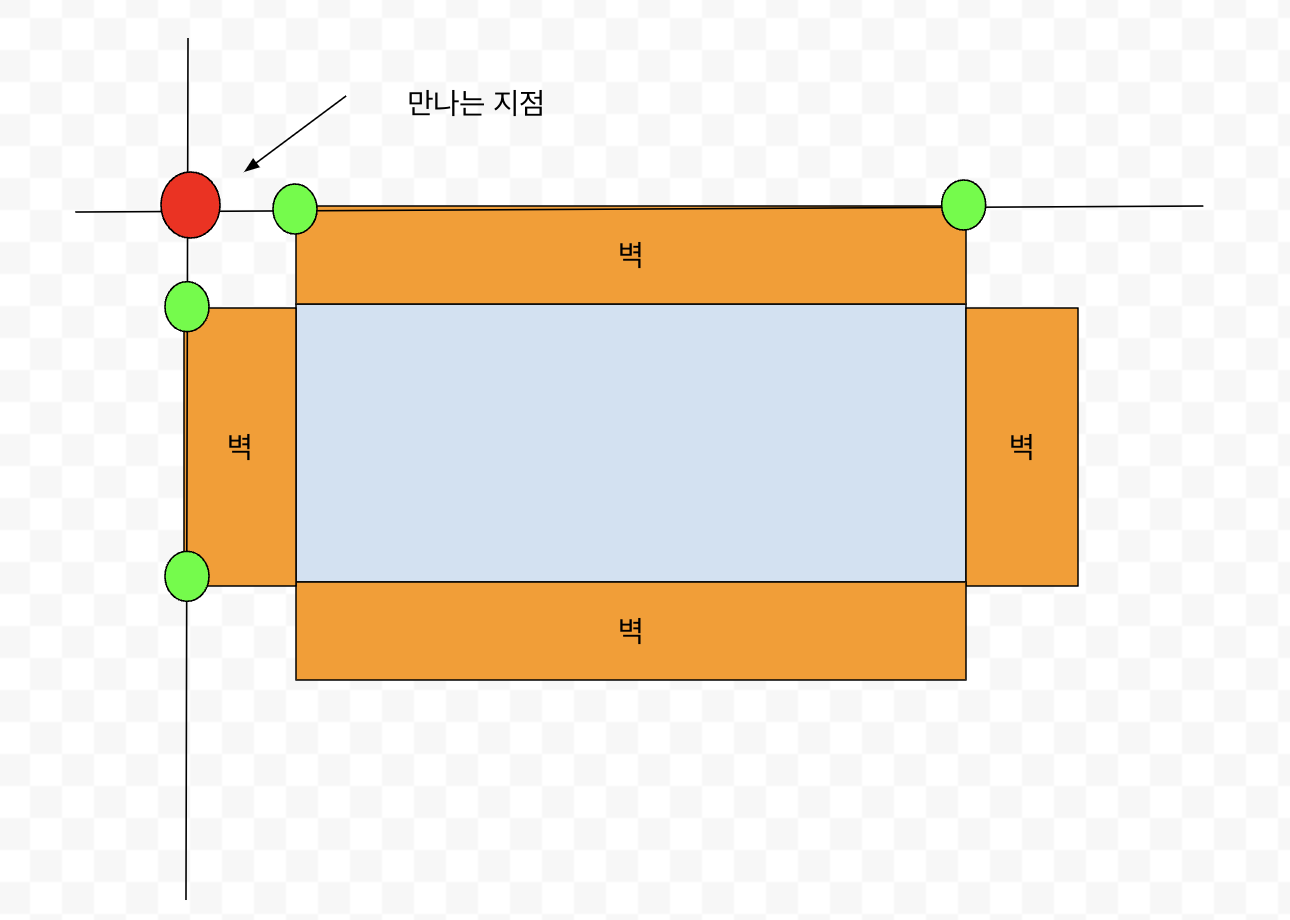
이제 저 만나는 지점의 좌표를 구해야합니다. 다행히 우리는 calculateOffsetPoints라는 함수로 한 변에 수평이 되는 직선의 두 좌표, 즉 초록색 원의 좌표들을 알고 있습니다.

교차점 구하기

우리는 각 변에서 offset만큼 떨어진 두 점 x1,z1과 x2,z2를 알고있습니다.

이 두 점을 변과 수평하는 직선을 그었을 때, 만나는 지점이 어디일까요?

우리는 중등수학을, 그 중에서 평면좌표계를 사용하여 그 값을 구할 수 있습니다.

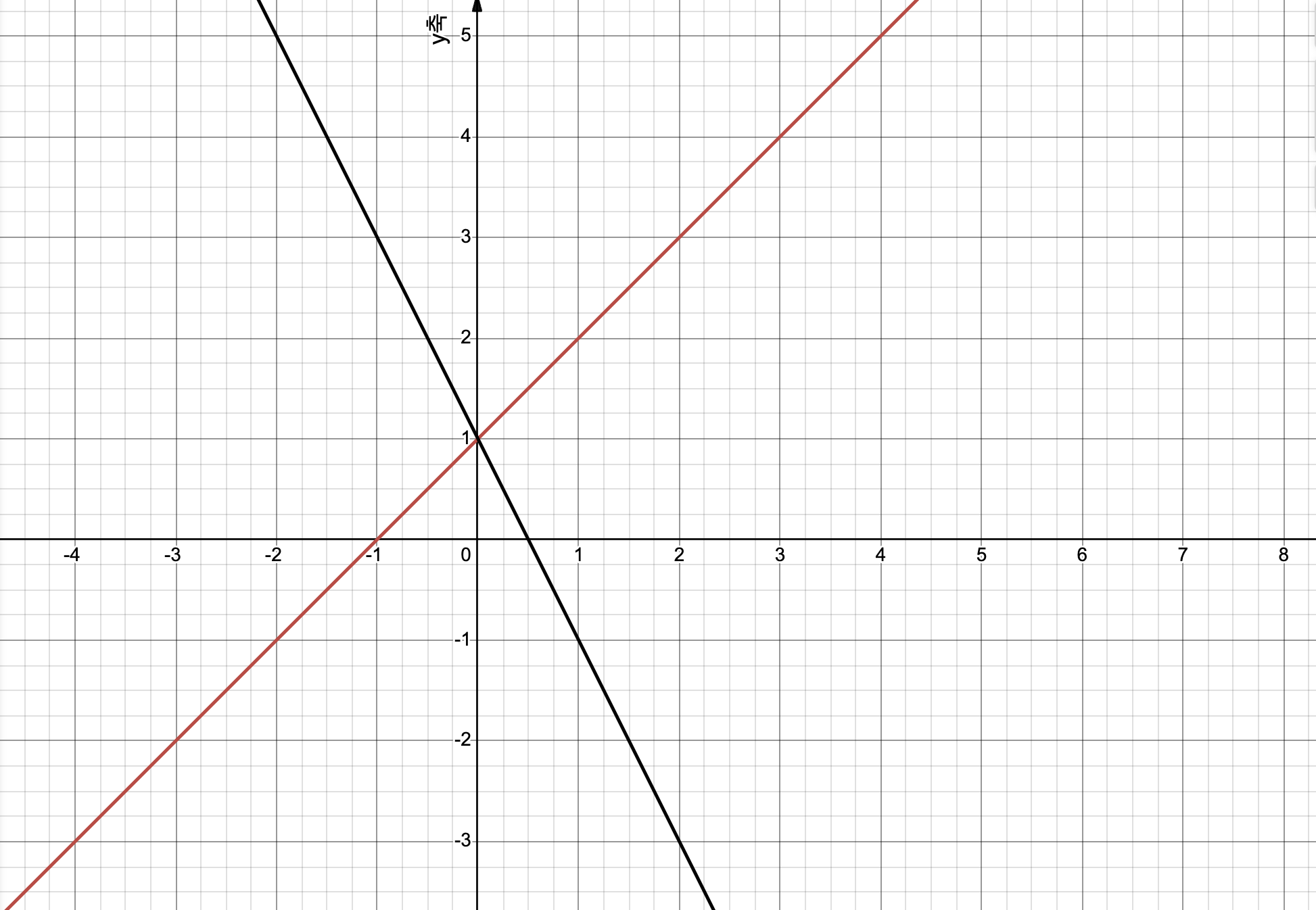
위 사진에는 두 직선이 있습니다. 빨간색 줄의 직선을 공식으로 나타내자면 y=x+1이고, 검은색 줄은 y=-2x+1입니다.

두 직선이 만나는 지점은 이 두 공식을 연립하여 구할 수 있습니다.

x + 1 = -2x + 1
x + 2x = 1 - 1
x = 0

위와같은 연립 방정식으로 x값을 구할 수 있습니다. 또한 이렇게 구한 x값을 두 공식 중 하나에 대입하면 y값도 구할 수 있습니다.

y = 0 + 1
y = 1

연립 방정식으로 우리는 (0,1)이라는 값을 구할 수 있습니다. 위 사진에서 두 직선이 만나는 지점이 같습니다.

하지만 우리는 좌표만 알고있지 공식은 알고있지 않습니다. 따라서 저희는 좌표를 토대로 공식을 구해야합니다.

우선 기울기(b)부터 구해보도록 하겠습니다.

b = (z2 - z1) / (x2-x1)

중등수학을 이용하면 손쉽게 기울기를 구할 수 있습니다. 기울기를 구했다면 절편값 또한 구할 수 있습니다.

아직 감이 안잡시히나요? 우리가 가진 조건을 정리해 보겠습니다.

우리는 x1,x2,z1,z2의 값을 알고있고 x3,x4,z3,z4의 좌표를 알고 있습니다.
두 좌표값을 알면 두 좌표를 지나는 직선의 공식을 구할 수 있습니다.
두 직선의 공식을 알고 있다면 두 직선의 교차점을 구할 수 있습니다.

이제 예시를 들어 설명해보겠습니다.

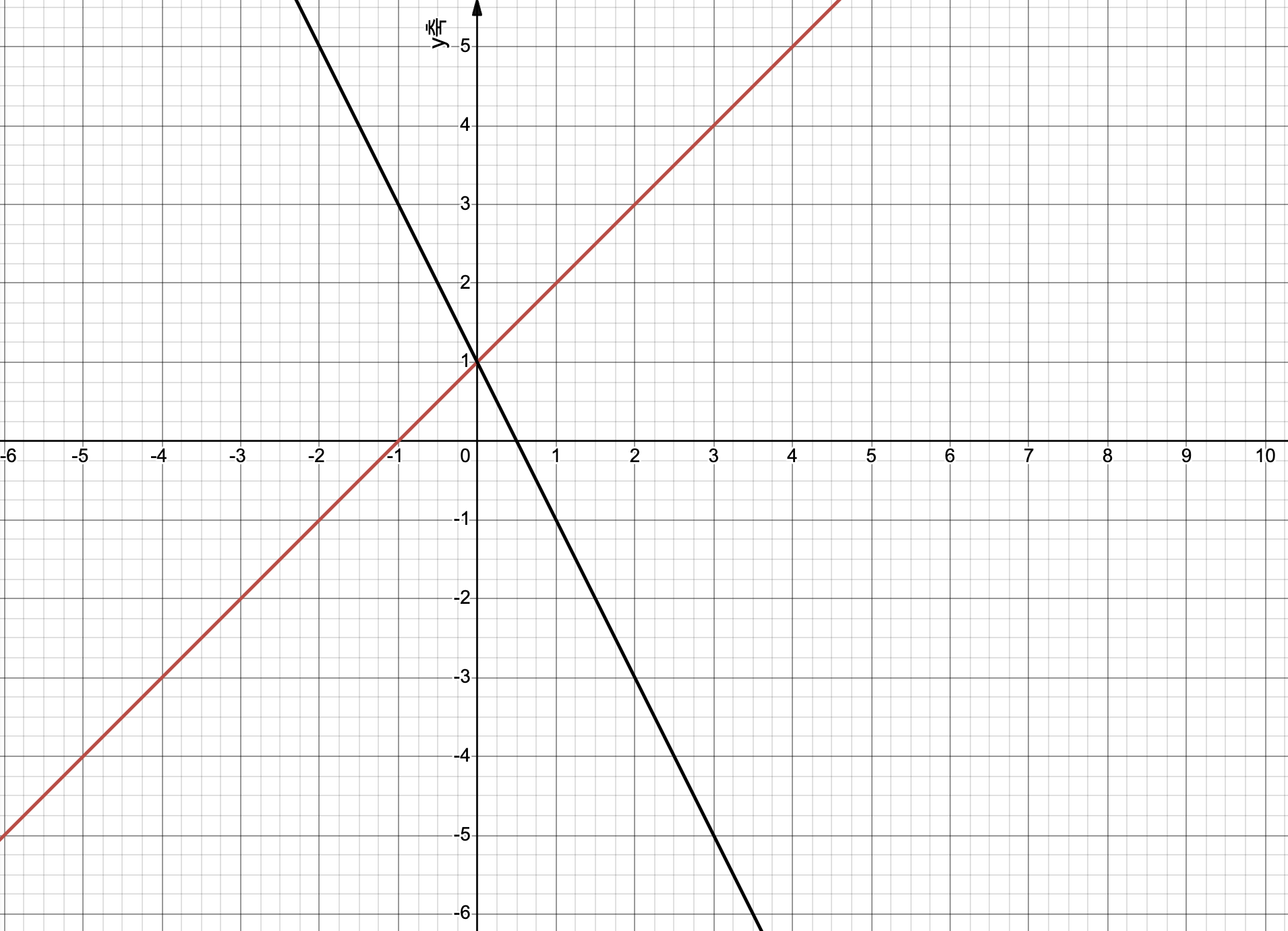
두 직선에서 좌표 두개를 각각 뽑아보겠습니다.

검은색 직선 (-1,3),(1,-1)
붉은색 직선 (-1,0),(1,2)

우선 저희는 y=bx + i와 같은 직선의 방정식을 구해야합니다. 하지만 저희가 알고있는 값은 x값과 y(z)값 입니다. 따라서 두 직선의 방정식을 구하기 위해 기울기과 절편값을 알아야합니다.

기울기(b)의 값은 설명한대로 두 좌표의 각각의 x값과 z값의 뺄셈으로 구할 수 있습니다. 우선 검은색 직선의 공식부터 구해보겠습니다.

b = (z2 - z1 ) / (x2 - x1) 
b = (-1 - 3) / (1 - (-1)
b = -2

다음은 절편을 구해보겠습니다.

y = bx + i
-1 = 1 * -2 + i
i = -1 + 2
i = 1

검은선의 방정식은 다음과 같습니다.

검은색 직선의 방정식
y = -2x + 1

같은 방식으로 붉은 선의 방정식 또한 구할 수 있습니다.

붉은색 직선의 방정식
y = 1x + 1

이제 두 직선의 방정식을 구했으니 이 두개의 방정식의 뺄셈이 바로 두 직선이 만나는 교차점입니다.

x 좌표

-2x + 1 = x + 1
-2x = x
x = 0

y 좌표
y = x + 1
y = 0 + 1
y = 1

좌표값 (0,1)이 사진상의 두 직선이 만나는 좌표와 같습니다.

방정식 또한 임의로 설정한 값과 맞아 떨어집니다.

이를 코드로 구현하면 매우 복잡한 과정입니다. 때문에 코드에서는 기울기-절편 형식의 방정식이 아닌 "일반형 방정식"을 사용합니다.

일반형 방정식은 다음과 같은 식입니다.

Ax + By = C

기울기-절편 형식의 방정식과는 조금 다르지만 기울기-절편 방정식을 위와같은 일반형 방정식으로 변환할 수 있습니다.

y = bx + i
-bx + y = i
bx - y + i = 0

이런 변환 과정을 코드로 작성하게되면 기울기-절편 방정식보다 더 쉽게 교차점을 계산할 수 있습니다.

export function caclulateIntersectionPoint(x1, y1, x2, y2, x3, y3, x4, y4) {
  // 선 1: (x1, y1)과 (x2, y2) 를 지나는 직선
  const A1 = y2 - y1; // y축 증가량
  const B1 = x1 - x2; // x축 증가량
  const C1 = A1 * x1 + B1 * y1; //일반형 방정식, c = Ax + By

  // 선 2: (x3, y3)과 (x4, y4) 를 지나는 직선
  const A2 = y4 - y3;
  const B2 = x3 - x4;
  const C2 = A2 * x3 + B2 * y3;

  // 두 직선의 계수로부터 교차점을 계산
  const determinant = A1 * B2 - A2 * B1;

  if (determinant === 0) {
    // 평행하거나 일치하는 경우 교차점이 없음
    // return null;
  }

  const x = (B2 * C1 - B1 * C2) / determinant;
  const y = (A1 * C2 - A2 * C1) / determinant;
  return { x, y };
}

코드는 위에 설명했던 대로 기울기-절편 방정식을 일반형 방정식으로 변환하여 교차점을 계산합니다.

y = (c1 - a1 * x) / b1
a2 * x + b2 * ((c1 - a1 * x) / b1) = c2
a2 * x + (b2*c1 = b2*a1 * x) / b1 = c2
모든 항을 정리하면,
(a2 - (b2 * a1) / b1) * x = c2 - (b2 * c1) / b1
x = (b2 * c1 - b1 * c2) / determinant
determinant = a1 * b2 - a2 * b1 즉, 
최종적으로 x의 값은 x = (b2 * c1 - b1 * c2) / determinant가 됩니다. 이를 통해 계산된교차점 좌표로 새 벽을 생성합니다.

~~이 공식을 코드로 작성하는데 있어 어려움이 있었고 최대한 간결하게 노력해보려 했지만 아직까지는 코드가 매우 복잡(더럽)습니다.~~

이제 외벽을 구현했으니 사용자가 어떤 모양의 방을 구현해도 외벽은 일정한 offset범위를 가지며 잘 동작하는 것을 볼 수 있습니다.

2-3. 3D파일 렌더

저희의 주요 기능 중 하나는 3D 파일을 화면상에 렌더링하는 것입니다. 3D파일이란 .gltf 혹은 .fbx등의 파일을 말하며 해당 파일을 통해 3D 객체를 불러와 렌더링할 수 있습니다.

다행히 Three.js는 3D 파일을 렌더링할 수 있는 기능을 지원합니다.

import { GLTFLoader } from "three/addons/loaders/GLTFLoader.js";

3D파일 렌더는 Three.js의 addons에서 지원합니다.

해당 Loader를 사용하면 다음과 같이 3D파일을 불러와 사용할 수 있습니다.

import { GLTFLoader } from "three/addons/loaders/GLTFLoader.js";

const loader = new GLTFLoader();

export const createChair = () => {
  return new Promise((res, rej) => {
    loader.load(
      "public/gltf/chair/chair.gltf",
      (gltf) => {
        res(gltf.scene);
      },
      undefined,
      (error) => {
        rej(error);
      }
    );
  });
};

export const loadFurnitures = Promise.allSettled([createChair()]);

gltf의 로드는 네개의 인자를 받습니다.

url: 로드할 파일의 경로
onLoad: 로드가 완료되면 호출되는 콜백 함수. 로드된 GLTF 모델이 인자로 전달됩니다
onProgress(optional): 로딩 진행 상황을 추적할 수 있는 콜백 함수.
onError: 로중 중 오류가 발생했을 때 호출되는 콜백 함수.

해당 메서드를 사용하여 우리는 손쉽게 3D파일을 렌더링할 수 있습니다.

2-4. 2D <-> 3D

우리는 2D로 작성된 방을 3D로 변환시켜 사용자에게 보여줄 수 있습니다.

이 기능은 OrbitControls라는 Three.js기능으로 만들 수 있습니다.

import { OrbitControls } from "three/addons/controls/OrbitControls.js";

const controls = new OrbitControls(camera, renderer.domElement);

이 OrbitControls는 카메라의 움직임을 마우스나, 터치 이벤트로 제어할 수 있께 해주는 컨트롤러입니다. 이를 통해 3D 장면에서 카메라가 특정 물체 주위를 회전하거나 확대/축소하는 기능을 쉽게 구현할 수 있습니다.

Three.js를 사용하셨던 분들은 아시겠지만 기본적으로 Three.js는 화면상의 차원은 3D입니다.

저희 또한 Three.js를 3D를 기본적으로 사용했는데요, 이를 2D 화면에서는 2D로 보이게 하기 위해 이 OrbitControls의 기능을 해제해주었습니다.

const controls = new OrbitControls(camera, renderer.domElement);
controls.enabled = false;

또한 카메라가 위에서 아래로 내려다보는 시점을 주기 위해 camera의 시점을 재정의했습니다.

camera.position.set(0, cameraZoom, 0);
camera.lookAt(0, 0, 0);

이를 통해 사용자가 모델링 페이지에 접속하게 되면 기본적으로 2D처럼 보이게 해줍니다.

2-4. WebGL사용이 안되는 환경이라면

모든 것은 사용자 환경에 따라 달라집니다. 즉, 게임을 개발하시는 분이라면, Apple또는 Google 등의 정책에 맞추어 개발을 진행 및 스토어 등록을 진행해야하고, 웹이라면 웹(Chrome, FireFox 등)에 따라 개발해야합니다.

우리 또한 "사용자가 WebGL을 사용할 수 없는 환경이라면..."이라는 의문을 품었습니다.

다행히 우리는 사용자가 WebGL을 사용할 수 있는 환경인지를 판별하는 코드를 공식 코드에서 발견할 수 있었습니다.

const WEBGL = {
  isWebGLAvailable: function () {
    try {
      var canvas = document.createElement("canvas");
      return !!(
        window.WebGLRenderingContext &&
        (canvas.getContext("webgl") || canvas.getContext("experimental-webgl"))
      );
    } catch (e) {
      return false;
    }
  },

  isWebGL2Available: function () {
    try {
      var canvas = document.createElement("canvas");
      return !!(window.WebGL2RenderingContext && canvas.getContext("webgl2"));
    } catch (e) {
      return false;
    }
  },

  getWebGLErrorMessage: function () {
    return this.getErrorMessage(1);
  },

  getWebGL2ErrorMessage: function () {
    return this.getErrorMessage(2);
  },

  getErrorMessage: function (version) {
    var names = {
      1: "WebGL",
      2: "WebGL 2",
    };

    var contexts = {
      1: window.WebGLRenderingContext,
      2: window.WebGL2RenderingContext,
    };

    var message =
      'Your $0 does not seem to support <a href="http://khronos.org/webgl/wiki/Getting_a_WebGL_Implementation" style="color:#000">$1</a>';

    var element = document.createElement("div");
    element.id = "webgl-error-message";

    if (contexts[version]) {
      message = message.replace("$0", "graphics card");
    } else {
      message = message.replace("$0", "browser");
    }

    message = message.replace("$1", names[version]);

    element.innerHTML = message;

    return element;
  },
};

// module.exports = { WEBGL }
export { WEBGL };

isWebGLAvailable: WebGl 1.0이 브라우저에서 지원되는지를 확인합니다. window.WebGLRenderingContext가 존재하는지 확인하고 canvas엘리먼트에서 "webgl" 또는 "experimental-webgl" 컨텍스트를 생성할 수 있는지 테스트합니다.
isWebGL2Available: WebGL2/0이 브라우저에서 지원되는지를 확인합니다. 마찬가지로 canvas 엘리먼트에서 "webgl2"컨텍스트를 사용할 수 있는지를 확인합니다.
getWeblGL2ErrorMessage: WebGL 2.0이 지원되지 않는 경우 사용자에게 오류를 표시합니다
getErrorMessage(version): version에 따라 WebGL 1.0 또는 2.0과 관련된 메세지를 만들어 반환합니다. 오류가 브라우저 때문인지 그래픽카드 때문인지 판단하여 메세지를 다르게 구성합니다.

위 코드를 사용하여 사용자가 페이지에 진입하면 해당 코드를 동작시켜 WebGL이 사용 가능한 환경인지 판별해주도록 합니다.

제가 중요하다고 생각한 부분은 위의 부분이 전부입니다. 후에 Three.js와 관련된 부분을 유지보수하며 생각이 난다면 추가하겠습니다.

평소에 프론트 또는 백엔드 개발을 진행하며 수학은 거의 사용하지를 않았습니다. 제가 깊게 개발을 하지 않은 탓도 있었으나 좌표계 등의 수학은 사용하지 않았죠. 그러나 이번 프로젝트를 진행하며 좌표계 수학을 사용했고 이에 대해 게임개발을 하는 친구와 이야기를 나눴습니다. 그 친구에게 들은 바로는 게임 개발은 기본적으로 고등수학(이과)까지 골고루 사용한다였습니다. 생각해보니 게임개발 또한 Three.js에서처럼 x,z,y축의 기준으로 물체를 설정하고 그에 따른 빛 조건, 텍스쳐, 물리엔진 등의 설계를 진행합니다. 실제 게임 개발은 더 많은 기능을 수학을 사용할지도 모르지만요.

개발을 시작할 때는 프론트엔드 개발자를 목표로 잡고 공부했고 동시에 서버에 흥미를 느껴 Node.js를 더불어 공부했습니다. 회사에서는 프론트엔드 개발을 주로 맡았으며 회사의 서버 개발자분에게 Python 서버개발을 배웠습니다. 이 프로젝트는 정말 오랜만에 수학의 재미를 느끼는 프로젝트였습니다. 더불어 많은 수학 개념을 사용하는 게임 개발에 흥미를 느꼈습니다. 아마 시간이 된다면 C#을 공부할지도 모르겠습니다.

저작자표시

'자바스크립트' 카테고리의 다른 글

threejs) 프레임마다 업데이트되는 TextGeometry (2)	2024.08.25
JS) 무한 캔버스(Infinity Canvas)의 원리와 구현 (1)	2024.06.30
React) mediasoup을 이용한 SFU (1)	2024.05.03
JS) 논리적 AND OR (0)	2024.04.16
JS) remove() 와 removeChild() (0)	2024.04.12

1일1개발공부

THREEJS로 인테리어 기능

목차

1. THREE.JS 소개

2. 프로젝트에 녹여낸 기능과 구현 방식

'자바스크립트' 카테고리의 다른 글

티스토리툴바

THREEJS로 인테리어 기능

목차

1. THREE.JS 소개

2. 프로젝트에 녹여낸 기능과 구현 방식

'자바스크립트' 카테고리의 다른 글

'자바스크립트' Related Articles

티스토리툴바